Сколько досок в кубе таблица 6 метров
Сколько в кубе досок длинной 6 метров. Ниже приведена таблица количества досок в кубе с размерами досок.
| Размер доски (6 метров) | Количество в кубе |
|---|---|
| Доска 20 мм (6 метров) | Количество штук |
| 20х100 | 83 |
| 20х120 | 69 |
| 20х150 | 55 |
| 20х180 | 46 |
| 20х200 | 41 |
| 20х250 | 33 |
| Доска 25мм (дюймовка) (6 метров) | Количество штук |
| 25х100 | 67 |
| 25х120 | 55 |
| 25х150 | 44 |
| 25х180 | 37 |
| 25х200 | 33 |
| 25х250 | 26 |
| Доска 30 мм (6 метров) | Количество штук |
| 30х100 | 55 |
| 30х120 | 46 |
| 30х150 | 37 |
| 30х180 | 30 |
| 30х200 | 27 |
| 30х250 | 22 |
| Доска 40 мм (6 метров) | Количество штук |
| 40х100 | 41 |
| 40х120 | 34 |
| 40х150 | 27 |
| 40х180 | 23 |
| 40х200 | 20 |
| 40х250 | 16 |
| Доска 50 мм (6 метров) | Количество штук |
| 50х100 | 33 |
| 50х120 | 27 |
| 50х150 | 22 |
| 50х180 | 18 |
| 50х200 | 16 |
| 50х250 | 13 |
| Поперечный размер досок | Кол-во в кубе |
Скачать Xlsx файл с количеством досок в кубе по ссылке: Скачать.
В таблице присутствует ссылка на каталог пиломатериалов нашего сайта RUS-LesDom.ru
Сколько Досок 25х150х6000 в 1 Кубе
Автор: Pavel Markovich
Быстрая навигация по статье (содержание)
- Сколько в Кубе Досок? — Таблица
- Сколько в кубе досок 25х150х6000? Как перейти от объема к количеству?
- Как определиться с объемом заказа
📝 Древесные материалы заказываются в мерах объема. За единицу измерения в этом случае берется, как правило, кубический метр (м3), в чем осуществляется учет при хранении таких материалов и выполнении погрузочно-разгрузочных работ.
Расчет досок 25х150х6000 в кубеНо часто бывает необходимым знание нужного количества деревянных изделий (досок, бруса, брёвен и т. д.) в штуках и сколько их насчитывается в единице объема.
Доски, как бревна с брусом, отличаются своими размерами, что осложняет их штучный учёт. Поэтому за стандартную единицу измерения принята мера объема — кубический метр (кубометр), представляющий собой многогранник с квадратными гранями, стороны которых равны метру.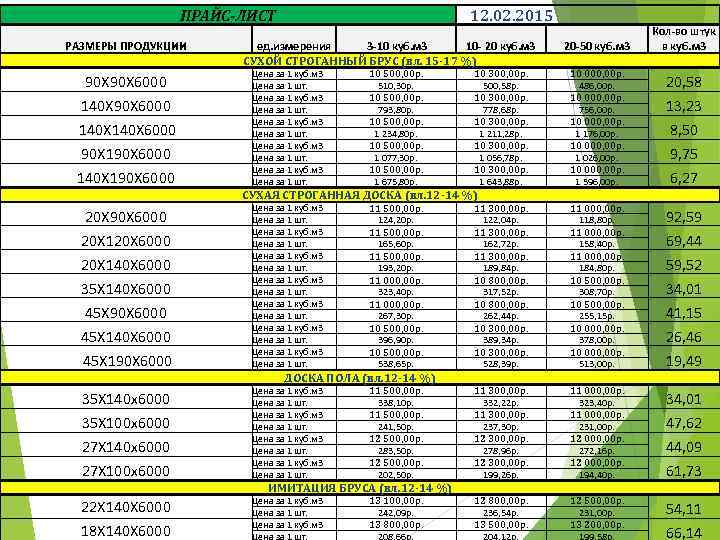
Для вычисления объема необходимо перемножить значения длины, ширины и высоты доски или ее площади на высоту (толщину). Если доски уложены в стопку, то для определения объема берутся ее габариты.
Таблица расчета досок:
| Размеры, мм | Объём досок в 1 м3 | Количество досок в м3 | Количество досок в м2 |
| 20 мм | |||
| 20х100х6000 | 0,012 м3 | 83 шт. | 50 м2 |
| 20х120х6000 | 0,0144 м3 | 69 шт. | 50 м2 |
| 20х150х6000 | 0,018 м3 | 55 шт. | 50 м2 |
| 20х180х6000 | 0,0216 м3 | 46 шт. | 50 м2 |
| 20х200х6000 | 0,024 м3 | 41 шт. | 50 м2 |
| 20х250х6000 | 0,03 м3 | 33 шт. | 50 м2 |
| 25 мм | |||
| 25х100х6000 | 0,015 м3 | 67 шт. | 40 м2 |
| 25х120х6000 | 0,018 м3 | 55 шт. | 40 м2 |
| 25х150х6000 | 0,0225 м3 | 44 шт. | 40 м2 |
| 25х180х6000 | 0,027 м3 | 37 шт. | 40 м2 |
| 25х200х6000 | 0,03 м3 | 33 шт. | 40 м2 |
| 25х250х6000 | 0,0375 м3 | 26 шт. | 40 м2 |
| 30 мм | |||
| 30х100х6000 | 0,018 м3 | 55 шт. | 33 м2 |
| 30х120х6000 | 0,0216 м3 | 46 шт. | 33 м2 |
| 30х150х6000 | 0,027 м3 | 37 шт.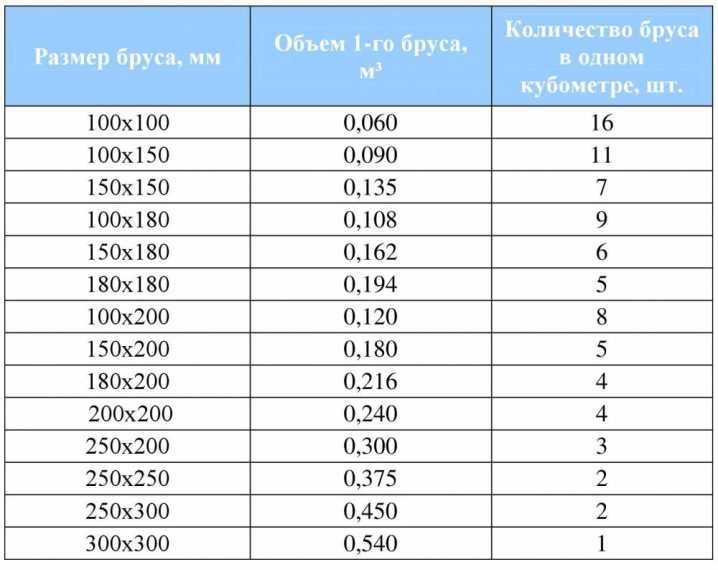 | 33 м2 |
| 30х180х6000 | 0,0324 м3 | 30 шт. | 33 м2 |
| 30х200х6000 | 0,036 м3 | 27 шт. | 33 м2 |
| 30х250х6000 | 0,045 м3 | 22 шт. | 33 м2 |
| 32 мм | |||
| 32х100х6000 | 0,0192 м3 | 52 шт. | 31 м2 |
| 32х120х6000 | 0,023 м3 | 43 шт. | 31 м2 |
| 32х150х6000 | 0,0288 м3 | 34 шт.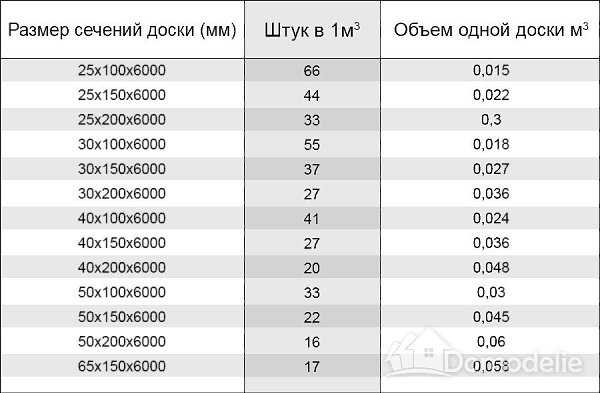 | 31 м2 |
| 32х180х6000 | 0,0346 м³ | 28 шт. | 31 м2 |
| 32х200х6000 | 0,0384 м3 | 26 шт. | 31 м2 |
| 32х250х6000 | 0,048 м3 | 20 шт. | 31 м2 |
| 40 мм | |||
| 40х100х6000 | 0,024 м3 | 41 шт. | 25 м2 |
| 40х120х6000 | 0,0288 м3 | 34 шт. | 25 м2 |
| 40х150х6000 | 0,036 м3 | 27 шт. | 25 м2 |
| 40х180х6000 | 0,0432 м3 | 23 шт.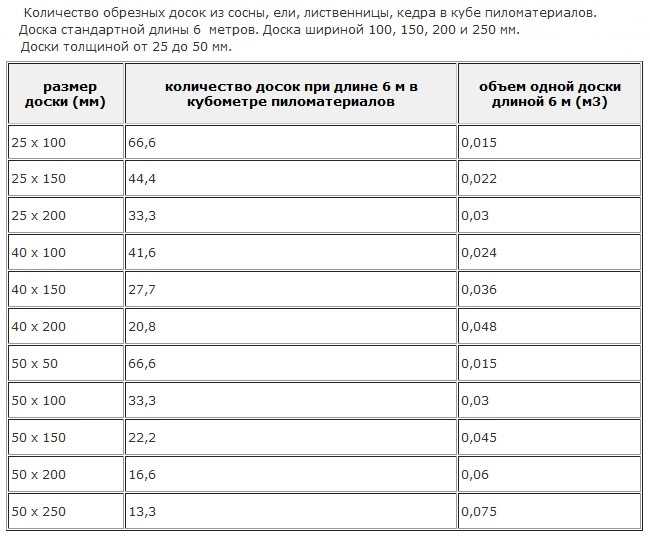 | 25 м2 |
| 40х200х6000 | 0,048 м3 | 20 шт. | 25 м2 |
| 40х250х6000 | 0,06 м3 | 16 шт. | 25 м2 |
| 50 мм | |||
| 50х100х6000 | 0,03 м3 | 33 шт. | 20 м2 |
| 50х120х6000 | 0,036 м3 | 27 шт. | 20 м2 |
| 50х150х6000 | 0,045 м3 | 22 шт. | 20 м2 |
| 50х180х6000 | 0,054 м3 | 18 шт.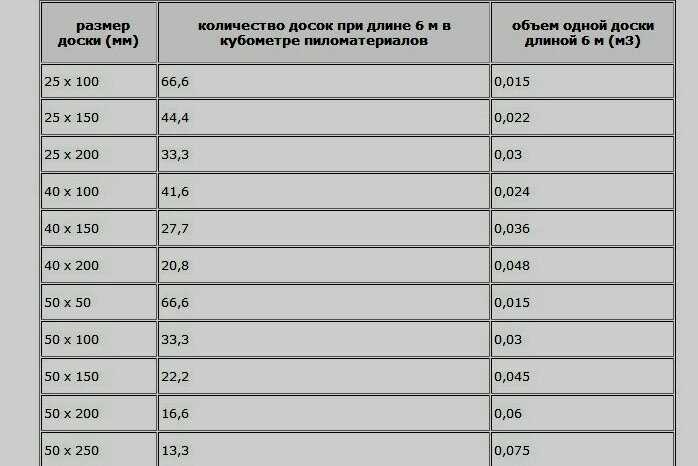 | 20 м2 |
| 50х200х6000 | 0,06 м3 | 16 шт. | 20 м2 |
| 50х250х6000 | 0,075 м3 | 13 шт. | 20 м2 |
Сколько в кубе досок 25х150х6000? Как перейти от объема к количеству?
В качестве примера имеется доска обрезная толщина, ширина и длина которой составляют в миллиметрах 25×150×6000 или в метрах 0.25×0,15×6. Для определения объема одной доски нужно перемножить размеры в метрах. В результате получится 0,0225 м3. Далее необходимо решить пример: 1: 0,0225 = 44,4 шт. Именно столько досок с 25 на 150 на 6000 размерами находится в одном кубометре.
Следует внимательно относиться к результатам в виде дробных чисел, т. к. нечестные продавцы строительных материалов могут этим воспользоваться для обмана, округляя их в выгодную для себя сторону.
При больших объемах это приводит покупателя к значительным потерям. Кроме этого, чтобы быть уверенным в достаточности приобретённых материалов нужно заказывать их с некоторым запасом.
Как определиться с объемом заказа
Для этого нужно знать потребное количество досок для выполнения каких-либо работ. Если, например, требуется настелить пол в помещении с размерами 4 на 2,25 м, то потребуется 15 досок длиной 4 метра (2,25: 0,15). Объём одной такой доски равен 0,015 кубометра (0,025*0,15*4). А объем 15 досок составят 0,225 м3 (0,015*15). Столько и нужно заказывать без учёта запаса, который может включать 2–3 доски. Тогда объем заказа составит не более 0,27 м3 (0,225 + 0,015*3).
На практике для определения количества досок применяются специальные таблицы (смотрите выше), включающие в себя размеры самых востребованных материалов. Для определения объема досок, имеющих разную ширину по всей длине, требуется методика, отличающаяся от приведённой выше. В этом случае доски укладываются в стопку так, чтобы ширина ее в разных концах отличалась незначительно.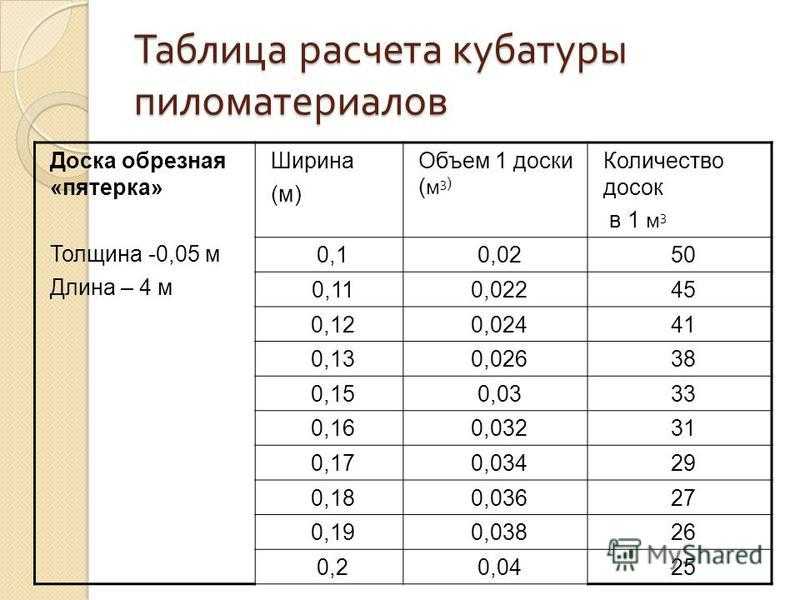
При этом методе учитываются воздушные зазоры, имеющиеся между отдельными досками, для чего полученный результат умножается на определенный коэффициент, зависящий от величины зазоров.
Сколько клеток на шахматной доске?
Сколько клеток на шахматной доске? В зависимости от вашей интерпретации, это может быть воспринято как вопрос с подвохом. Ответ 64 квадрата (8×8) совершенно верен, но есть и альтернативный ответ, если мы посчитаем квадраты разных размеров, а не только отдельные квадраты.
Например, есть один квадрат размером 8×8 единиц:
Тогда есть четыре квадрата размером 7×7 единиц:
И девять квадратов размером 6×6 единиц:
Я уверен, что вы уже видели узор. По мере того, как мы постепенно уменьшаем целевой квадрат на одну единицу, мы можем найти идеальный квадрат несколько раз. Имеется 2×2 начальных позиций, с которых может начинаться (7×7) клеток, имеется 3×3 начальных позиций, с которых может начинаться (6×6) клеток …
Общее количество квадраты таким образом:
Существует также формула для быстрого вычисления суммы квадратов.
Для шахматной доски с n=8 мы видим, что сумма равна 204.
Интересно, что по мере увеличения n эта формула стремится к n 3 /3 . Я уверен, что из этого есть какие-то особенно крутые последствия, но я не могу придумать ни одного в данный момент. Если вы думаете об одном, напишите мне, и я обновлю эту страницу и отдам вам должное!
Обновление!
Изображение: Изабель призывает к миру всех студентов-историков Кредит: Рэйчел
Я получил приятное электронное письмо от Маноса Камарианакиса, который предложил следующее:
«Следствие суммы n 2 , стремящейся к n 3 /3. Это оказывается довольно просто и увлекательно! Считайте, что каждому числу n 2 соответствует n 2 маленьких кубиков размера 1 , сложим таким образом, чтобы образовался квадрат. Для каждого n=1,2,3,… положим эти квадраты друг на друга (нет необходимости центрировать их, благодаря теореме Фубини).
Если мы будем повторять этот процесс бесконечно , мы действительно можем «видеть» формирование пирамиды, объем которой действительно равен n 3 /3 = сумме объемов кубов!»
Нашла в интернете картинку такого зиккурата, сделанного из кубиков сахара!
Прямоугольники
Как насчет количества прямоугольников на шахматной доске? Что ж, чтобы сделать прямоугольник, вам нужно выбрать любые две вертикальные линии и любые две горизонтальные линии. Есть 9 C 2 пары горизонтальных линий, которые вы можете выбрать (36 различных пар), и столько же вертикальных пар, поэтому ответ 36 × 36 = 1296.
Вот таблица первых нескольких квадратных сеток и количество квадратов и прямоугольников:
| Board Size | # Squares | # Rectangles |
|---|---|---|
| 1×1 | 1 | 1 |
| 2×2 | 5 | 9 |
| 3×3 | 14 | 36 |
| 4×4 | 30 | 100 |
| 5×5 | 55 | 225 |
| 6×6 | 91 | 441 |
| 7×7 | 140 | 784 |
| 8×8 | 204 | 1,296 |
| 9×9 | 285 | 2,025 |
| 10×10 | 385 | 3,025 |
Реклама:
2002 Головоломка
Все началось с того, что я наткнулся на старую головоломку, созданную, приписываемую Эриху Фридману, в 2002 году:
Возьмите сетку из 18×18 квадратов и удалите два из них так, чтобы полученная фигура содержала ровно 2002 квадрата всех размеров, составленных из оставшихся квадратов.
В Интернете есть ответ, но я не мог с ним согласиться, поэтому написал немного кода, чтобы сгенерировать все ответы.
Если вы хотите попробовать сами, вот апплет ниже. В этом варианте вы также можете указать различные размеры сетки и количество заштрихованных блоков, которые вам разрешено устанавливать.
Решения
Вы нашли решение? Если вы хотите увидеть все 64 решения (, а не , дедублированные поворотами или отражениями), нажмите ниже.
Хорошие задачи – Peter Liljedahl
Это задачи, выбранные из множества ресурсов. По возможности я буду указывать источник, из которого оно пришло. Решений здесь не будет, но если вы перейдете по ссылке на источник, то там могут быть решения.
Складной змей #1
Из бумаги какого размера можно сложить бумажного змея?
Дуэльный кубик
- Красный: 0, 1, 7, 8, 8, 9
- Синий: 5, 5, 6, 6, 7, 7
- Зеленый: 1, 2, 3, 9, 10, 11
- Черный: 3, 4, 4, 5, 11, 12
Используются для игры вдвоем.
Игрок 1 выбирает один из кубиков для игры. Затем игрок 2 выбирает кубик. Теперь каждый игрок бросает свой кубик. Игрок с наибольшим показанным числом получает очко. Первый игрок, набравший 7 очков, выигрывает игру. Если вы игрок 1, какую смерть вы должны выбрать. Если вы игрок 2, какой кубик вы должны выбрать? [из Центра задач по математике]
Арифметический ряд
Найдите сумму арифметического ряда 13 + … + 61.
Потерянные простые числа
Три карты (см. ниже), каждая из которых имеет простое число на обратной стороне. Сумма чисел на лицевой и оборотной сторонах каждой карты такая же, как и на других картах. Какие числа указаны на обратной стороне каждой карты?
Перемешанные игральные кости
Представьте себе обычный шестигранный кубик и обратите внимание, что сумма противоположных граней всегда равна семи. Единица напротив шестерки, двойка напротив пятерки и так далее. Теперь представьте, что вы делаете свой собственный шестигранный кубик, не имеющий этого ограничения.
Сколько разных игральных костей можно было сделать?
Окрашенный куб
Покрасьте все стороны куба 3 x 3 x 3. Как только он высохнет, разберите его на кубики 1 x 1 x 1. Сколько из этих единичных кубов имеют краску на трех гранях? Два лица? Одно лицо? Без лиц? Исследуйте 4 x 4 x 4 и т. д.
Дифференцируемая функция
Рассмотрим дифференцируемую функцию ниже. Что такое м и б ?
Игра с шайбой
Таймер для яиц
Как приготовить яйцо за 9 минут, если у вас есть только таймер на 4 и 7 минут?
Кубик Рубика
ish У вас есть 27 маленьких кубиков, по 3 каждого из девяти цветов.
Квадратный штифт в круглом отверстии
Что лучше подходит: квадратный штифт в круглом отверстии или круглый штифт в квадратном отверстии?
Шахматная доска
Сколько клеток на шахматной доске? Сколько прямоугольников?
Последнее число
Рассмотрим строку 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Вычеркните любые два числа из этого списка и добавьте разницу в конец списка. Этот новый номер теперь является частью списка. Продолжайте процесс зачеркивания двух чисел в списке и прибавления разницы, пока не останется только одно число. Что можно сказать о последнем номере? Исследовать. [от Ричарда Хосино]
Настольный календарь
Какие числа должны быть в приведенном ниже настольном календаре, чтобы каждая дата от 01 до 31 могла быть представлена?
Пираты и Алмаз
Банда из 10 пиратов собирается распасться.
Они поделили все свое золото, но остался один ГИГАНТСКИЙ бриллиант, который нельзя разделить. Чтобы решить, кому достанется, капитан ставит всех пиратов (включая себя) в круг. Затем он указывает на одного человека, чтобы начать. Этот человек выходит из круга, берет свое золото и уходит. Человек слева от него остается в кругу, но выходит следующий человек. Это продолжается с уходом каждого второго пирата, пока не останется только один. На кого должен указать капитан, если он хочет убедиться, что алмаз останется у него? Что, если бы было 11 пиратов? Что, если бы было 12 пиратов? Что, если бы было 27 пиратов?
Предки медоносных пчел
У медоносных пчел очень интересная генеалогия. В то время как самки медоносных пчел появляются из оплодотворенных яиц, самцы медоносных пчел появляются из неоплодотворенных яиц. То есть у пчел-самок есть мать и отец, а у пчел-самцов — только мать. Посмотрите на генеалогическое древо самца медоносной пчелы. Сколько предков в предыдущем поколении? Тот, что был до этого? Тот, что был до этого? Сколько предков 10 поколений назад?
Пересечение моста
Адам, Боб, Клэр и Дейв гуляют: они подходят к старому покосившемуся деревянному мосту.
У них есть только один факел, и его нельзя бросить. Из-за разного уровня физической подготовки и некоторых незначительных травм все они могут преодолевать препятствия с разной скоростью. Адам может перейти за 1 минуту, Боб за 2 минуты, Клэр за 5 минут, а Дэйв за 10 минут.
Адам, мозги группы на мгновение задумываются и объявляют, что переправу можно пройти за 17 минут. Нет никакой хитрости. Как это делается? [от Найджела Колдуэлла]
Периметр треугольника
Определите минимальный периметр треугольника с одной вершиной в точке (7,1), одной вершиной на оси x и одной вершиной на линии y = x. [от Ричарда Хосино]
Пересекающиеся наборы
Поместите 17 предметов в два круга ниже, чтобы в каждом кругу было одинаковое количество предметов.
Сколько способов вы можете сделать это?
Что делать, если вы хотите, чтобы отношение объектов в одном круге к другому кругу было 4:3 или 12:9?
1001 пенни
На столе в ряд стоит 1001 пенни. Я прихожу и заменяю каждую вторую монету пятаком. Затем я заменяю каждую третью монету десятицентовиком. Наконец, каждую четвертую монету я заменяю на четвертак. Сколько денег на столе?
Расставьте карты в кадре
Разложите десять игральных карт (от туза до десятки) в прямоугольник с тремя картами с двух сторон и четырьмя картами с двух сторон так, чтобы сумма карт на каждой стороне была одинаковой. [от Аннет Руло]
Палиндромы
Рассмотрим число 28. Это не палиндром. Итак, я переворачиваю число и складываю его само с собой (28 + 82 = 110). 110 не палиндром. Итак, я переворачиваю его и добавляю сам к себе (110 + 011 = 121). 121 — это палиндром. Это означает, что 28 — это палиндром глубины 2 (чтобы сделать его палиндромом, потребовалось две итерации).
Какова глубина всех двузначных чисел?
Вероятность доски для дротиков
Два дротика брошены в круглую цель. Куда должен приземлиться первый дротик, чтобы вероятность того, что второй дротик окажется ближе к центру, составляла 50 %?
День Канады
В День Канады Алекс складывает кости друг на друга, пока сумма видимых граней не будет равна году. Когда он в следующий раз сможет это сделать? Обобщать.
10 Освобождение заключенных
Начальник тюрьмы решил, что его тюрьма переполнена, поэтому он хочет освободить некоторых заключенных. Его стратегия для этого заключается в том, что он берет десять заключенных наугад и выстраивает их в ряд так, чтобы каждый заключенный мог видеть только заключенных перед собой. Затем надзиратель наденет на голову каждого заключенного черную или белую шляпу. Начиная с конца ряда, надзиратель спросит заключенного, какого цвета у него шляпа. Если он угадывает правильно, то его отпускают. Затем надзиратель переходит к следующему заключенному в очереди и так далее.
Десяти заключенным разрешается встретиться, чтобы обсудить, прежде чем они выстроятся в очередь. Если они умны, они придумают стратегию, которая гарантированно спасет некоторых из них. Сколько вы могли бы спасти?
Фантастическая четверка
Составьте числа от 1 до 30, используя четыре четверки и любые операции.
Исходные числа
Рассмотрим два целых числа (например, 3 и 6). Это будут первые два числа. Третье число является суммой первых двух (9). Четвертый — это сумма двух предыдущих (15) и так далее (3, 6, 9, 15, 24, 39, …). Какими должны быть первые два числа, чтобы пятое число было 100?
Барсук Баки
Барсук Баки — талисман школьной футбольной команды. Каждый раз, когда его команда набирает очки, Баки делает количество отжиманий, равное общему количеству очков его команды на тот момент. Если его команда набрала 50 очков, сколько отжиманий мог сделать Баки? [от Дэна Мейера].
Охота на сусликов
Представьте себе серию равноотстоящих нор, тянущихся бесконечно вдоль линии в обоих направлениях.
Сурок находится в одной из нор и каждую минуту прыгает в новую дыру, которая находится на некотором фиксированном интервале дыр от его текущей норы. Вы не знаете, где он стартует, или интервал, через который он прыгает, или направление, в котором он идет, но после каждого его хода вы можете посветить фонариком в одно (и только одно) отверстие. Проблема состоит в том, чтобы найти метод, с помощью которого вы гарантированно найдете сурка.
Сумма 51
Сколько существует шестизначных чисел, сумма цифр которых равна 51? [из практики Ферма № 4, № 7]
Вогнутые многоугольники
Мы знаем, что сумма внешних углов любого выпуклого многоугольника равна 360º. Но что, если многоугольник вогнутый? Какие корректировки или дополнения к «правилу» необходимо сделать, чтобы сумма по-прежнему равнялась 360º? [от Роберта МакГрегора на AAMT]
Удлиненная золотая цепь
Вы путешествуете по Европе. У вас остался месяц до вылета домой, но у вас закончились деньги.
Однако у вас есть золотая цепочка из 50 звеньев, и вы нашли отель, который готов принимать одно звено за ночь для оплаты проживания и питания. Тем не менее, менеджер хочет оплаты каждый день, и он готов помочь вам, разрезая ссылки для вас. Проблема в том, что он хочет получить одну золотую плату за каждую ссылку, которую он вырезает. Какое наибольшее количество ссылок останется у вас, когда вы полетите домой? [мое расширение TestFunda vol. 1 (стр. 1)]
105
Сколькими способами число 105 можно представить в виде суммы по крайней мере двух последовательных положительных целых чисел? [из Canadian Team Math Contest, 2014, #12]
Налоговик
Налоговик Играется так: Начните с набора зарплатных чеков, от 1 до 12 долларов. Вы можете оставить себе любую зарплату. После того, как вы выберете, сборщик налогов получит все оставшиеся зарплаты, которые являются коэффициентами выбранного вами числа. Сборщик налогов должен получать оплату после каждого перемещения.
Если у вас нет ходов, которые дают сборщику налогов зарплату, то игра окончена, и сборщик налогов получает все оставшиеся зарплаты. Цель состоит в том, чтобы победить сборщика налогов.
Пример:
Ход 1: Возьмите 8 долларов. Сборщик налогов получает 1 доллар, 2 доллара и 4 доллара.
Ход 2: возьмите 12 долларов. Сборщик налогов получает 3 и 6 долларов (остальные множители уже учтены).
Ход 3: возьмите 10 долларов. Сборщик налогов получает 5 долларов.
У вас больше нет разрешенных ходов, поэтому игра окончена, и сборщик налогов получает 7, 9 и 11 долларов — оставшиеся чеки.
Всего баллов:
Вы: 8$ + 12$ + 10$ = 30$.
Сборщик налогов: 1 доллар + 2 доллара + 3 доллара + 4 доллара + 5 долларов + 6 долларов + 7 долларов + 9 долларов+ 11 долларов = 48 долларов.
Вопросы:
Можно ли победить сборщика налогов в этой игре на 12 долларов? Если да, то как? Какой максимальный балл вы можете получить?
Бонус: что, если вы играли в игру с зарплатой от 1 до 24 долларов? Как насчет от 1 до 48 долларов? [из Numberplay, 13 апреля]
Зерновые призы
Предположим, в вашей любимой коробке с хлопьями находится один из шести призов.
Возможно, это ручка, пластиковый персонаж фильма или карточка с изображением. Сколько коробок хлопьев вы должны купить, чтобы получить все шесть призов? [от Джорджа Риза]
Четыре туза
Разгадай карточный фокус с четырьмя тузами. [от Питера Лильедала]
Горящая веревка
У вас есть две веревки, каждая из которых горит два часа, если зажечь ее с одного конца. Эти веревки неоднородны, и некоторые части веревок сгорают быстрее, чем другие. Можете ли вы использовать веревки, чтобы выждать 1 час 30 минут? 45 минут? Какие еще времена вы могли бы получить? [из TestFunda, книга 1, № 7]
Сколько семерок
Если вы выпишите числа от 1 до 1000, сколько раз вы напишете число 7?
Оркестр
Учащиеся оркестра хотят выстроиться в очередь на свое выступление. Проблема в том, что когда они выстраиваются в линию по 2, остается 1 лишняя. Когда они выстраиваются в ряд по 3, остается 2 лишних. Когда они выстроятся в 4, останется 3. Когда они выстраиваются в ряд по 5, остается 4.
Когда они выстраиваются в ряд по 6, остается 5. Когда они выстраиваются в 7-е, учеников не остается. Сколько там студентов? [от Джона Гранта Маклафлина]
Следы шин
– Этот след, как вы понимаете, оставил всадник, который ехал со стороны школы, – заметил Шерлок Холмс.
– Или к нему? – сказал Ватсон.
– Нет, нет, мой дорогой Ватсон… Он, несомненно, направлялся прочь от школы. [от Джейми Малхолланда – презентация на CMEF 2014].
Пиратские шляпы
Жила-была группа пиратов во главе с капитаном Фрэнсисом Верней. Однажды ночью Фрэнсису задали вопрос, кто из группы будет достаточно умен, чтобы возглавить группу после того, как он уйдет.
Поэтому он решил провести серию тестов, чтобы найти самый умный. Как мы все знаем, проверить интеллект пиратов не так просто, поскольку они умны и рациональны по своей природе.
Фрэнсис берет 9 шляп, смесь белых и черных шляп. Он надел шляпы на головы 9 пиратов и сказал им, что они не должны разговаривать, и есть по крайней мере 1 белая шляпа, а черных шляп больше, чем белых.
Очевидно, что они не могут видеть свою шляпу, но они могут видеть цвет других 8 шляп. Если они ошибутся, им взорвут голову. Фрэнсис дал им 20 минут, чтобы разобраться, но никто не смог.
Так он дал еще 10 минут. Но все равно все держались тихо. Наконец он дал им 5 минут, и в конце все 9 узнали цвет своей шляпы, и все ответили одновременно. Подумайте о логике, которую использовали пираты. [из БЛОГА |V|UR@|_I’S – 17 июня 2013 г.]
Черные и белые шарики
Мы помещаем в ящик тринадцать белых шариков и пятнадцать черных. У нас также есть двадцать восемь черных шариков вне ящика. Достаем из коробки два шарика. Если они имеют другой цвет, мы кладем белый обратно в коробку. Если они одного цвета, мы кладем в коробку черный шарик. Продолжаем делать это до тех пор, пока в коробке не останется только один шарик. Какого он цвета? [из Вектора 55 (1) — с. 49]
Касательные многоугольники
На диаграмме изображены различные правильные многоугольники P, стороны которых касаются окружности C.
Покажите, что для любого правильного многоугольника, нарисованного таким образом:
[из журнала MEI Maths Item of the Month — март 2014 г.]
100 Делится
При делении 100 на натуральное число x получается остаток 10.
Три кувшина
Три кувшина емкостью 8, 5 и 3 литра соответственно. 8-литровый кувшин полностью заполнен водой, а два других кувшина пусты. Ваша задача — путем декантации разделить воду на две равные части, то есть 4 литра в кувшине A и 4 литра в кувшине B, оставив самый маленький кувшин пустым. [из MathXTC — Neurological Nasties (набор задач 9, # 3)]
Сбежавший заключенный
Сбежавший заключенный оказывается посреди квадратного бассейна. Охранник, который преследует его, находится в одном из углов бассейна. Охранник может бежать быстрее, чем заключенный может плавать.
Заключенный может бежать быстрее, чем охранник. Охранник не плавает. В каком направлении должен плыть заключенный, чтобы максимизировать вероятность того, что он сбежит? [из Вектора 54(2) – с. 95]
Золотая цепочка
Состоятельный человек должен был заплатить каменщику, строящему его дом. У него заканчивались деньги, поэтому он решил заплатить каменщику золотой цепью из 7 звеньев. Гонорар каменщика равнялся одному золотому звену каждый день. Богатый человек должен был платить каменщику каждый день, иначе он перестанет работать. Но в то же время он не хотел платить каменщику больше одного звена в день, потому что он мог убежать и не вернуться.
Разрезать цепь было очень сложно. Какое минимальное количество разрезов может сделать богатый человек в цепи и при этом платить каменщику каждый день в течение семи дней?
[из TestFunda vol. 1 (стр. 1)]
Скрученная веревка
Представьте себе кусок веревки, лежащий на столе перед вами. Поперечное сечение веревки представляет собой правильный многоугольник с N сторонами.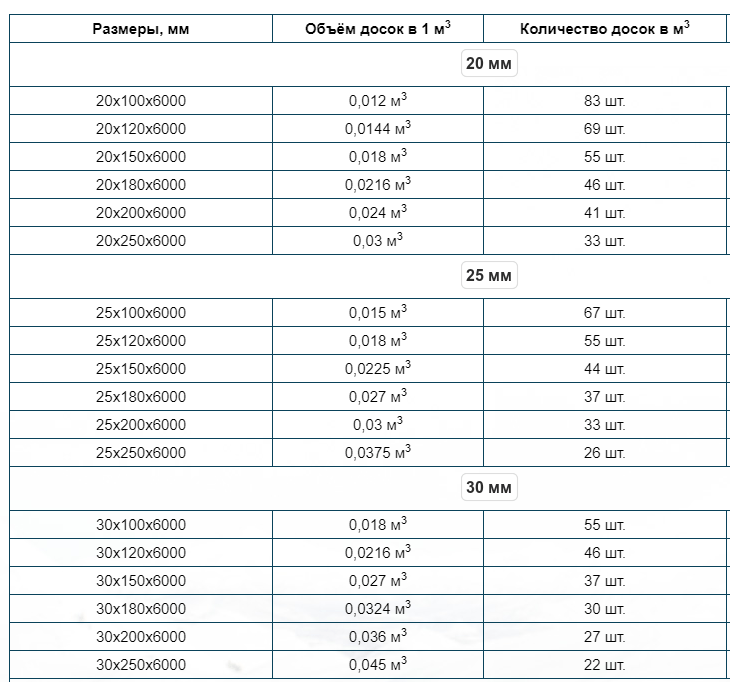
Сдвиньте концы веревки к себе так, чтобы она почти образовала круг.
Теперь мысленно возьмитесь руками за концы веревки. Вы собираетесь склеить концы веревки вместе, но перед этим поверните правое запястье так, чтобы многоугольный конец повернулся на одну n часть полного оборота. Повторите скручивание в общей сложности T раз, чтобы ваше мысленное запястье повернулось на T n долей полного оборота. ТЕПЕРЬ склейте концы вместе, чтобы многоугольные концы совпадали с ребрами, приклеенными к ребрам.
Когда ментальный клей высохнет, начните рисовать одну грань (плоскую поверхность) веревки и продолжайте, пока не обнаружите, что закрашиваете уже окрашенную часть. Начните снова с другой грани, еще не окрашенной, и используйте другой цвет.
Сколько цветов вам нужно?
[из «Математического мышления» (2-е издание) — Мейсон, Бертон и Стейси (стр. 103)]
Мостовой переход
Пять человек стоят по одну сторону моста.
Они хотят перейти мост.
Без факела они не могут двигаться дальше.
Доступен только один факел.
Оставшийся срок службы батареи фонарика составляет всего 30 секунд.
Одновременно по мосту могут пройти только два человека.
Факел нужно вернуть оставшимся людям.
Пять человек пересекают мост в разное время.
Чтобы пересечь мост, требуется 1 секунда.
Остальные занимают 3 секунды, 6 секунд, 8 секунд и 12 секунд.
Все пересекают мост в течение 30 секунд.
Как они поступают?
[из Головоломки II]
Небоскребы
- Вы должны заполнить сетку так, чтобы каждая строка и столбец содержали числа от 1 до 4.
- Каждая строка и столбец содержат каждое число только один раз.
- Тем не менее, вы должны следовать правилам снаружи, которые говорят вам, сколько небоскребов вы можете увидеть.
- Невозможно увидеть более низкий небоскреб за более высоким.
- Головоломки могут быть довольно сложными, и для их решения могут потребоваться приемы судоку.
